Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- geojson
- 이미지빌드
- Python
- osmnx
- 귀여운고래
- 도커 레이어
- python최단거리
- 지하철역좌표
- 컨테이너
- Set
- GIS
- 도커
- 알고리즘
- 동명이인찾기
- 좌표거리
- 패치분할
- 3d
- graph
- MESH
- 데이터입수
- GNN
- 그리드분할
- STL
- 폴더조사
- geopandas
- GCN
- 파이썬
- 3d데이터
- pyvista
- docker
Archives
- Today
- Total
이것저것 기록
[알고리즘] 병합 정렬 본문
* <모두의 알고리즘 with 파이썬>의 문제 10을 정리한 내용입니다.

1. 병합 정렬이란?
- 입력을 두 개로 분리하고 각각 해결한 다음, 이 결과를 모아서 원래의 문제를 해결하는 전략이다.
- 대개 재귀 호출을 이용하여 구현한다.
- 일반적으로 다음과 같은 과정을 거친다.
- 분할: 입력 데이터를 2개로 분할한다. 이때, 파이썬에서는 // 연산자를 사용한다.
- 정복: 부분 데이터를 정렬한다.
- 결합: 정렬된 부분 배열을 다시 하나의 배열에 합병한다.
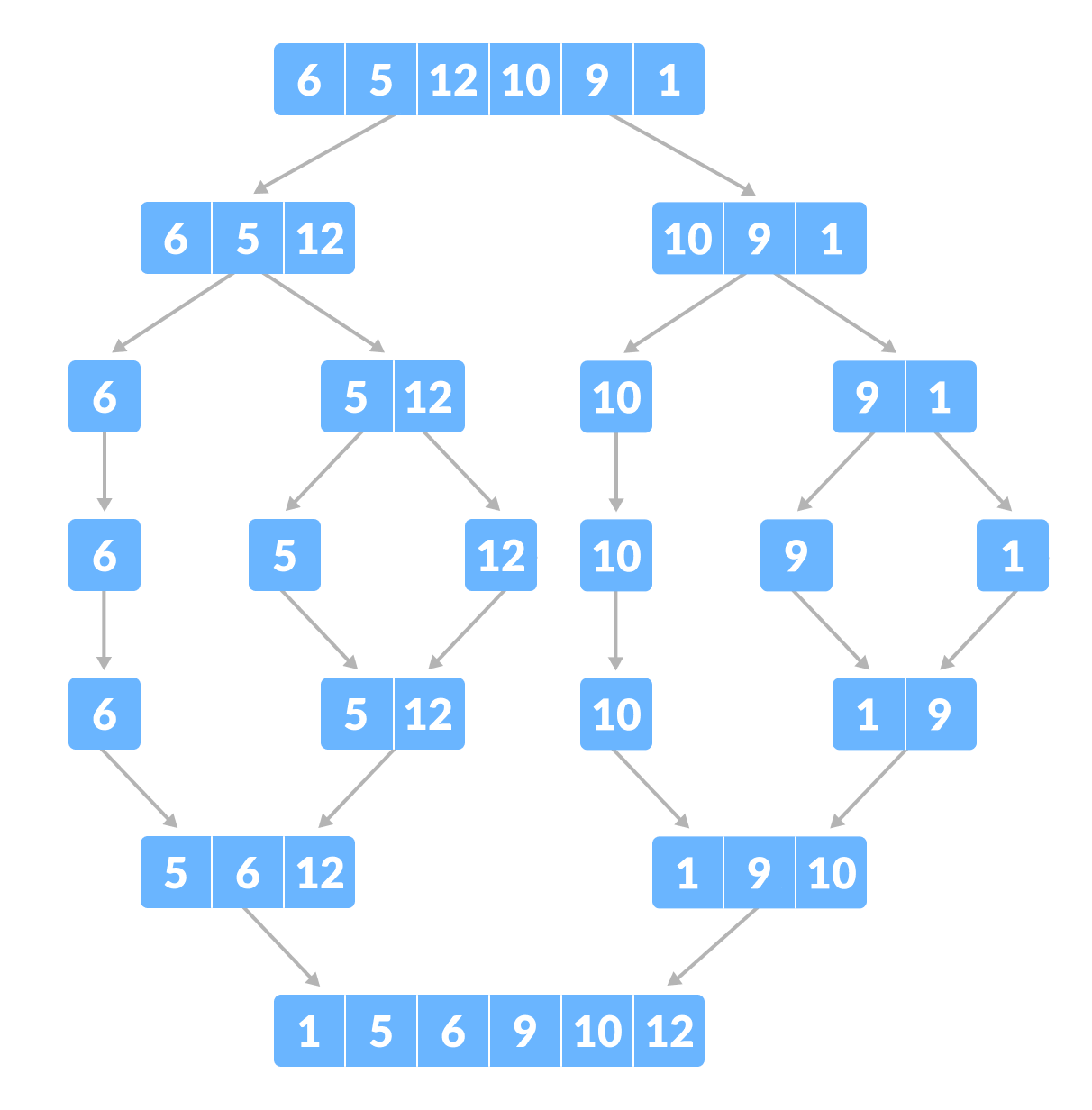
- 아래 그림에서 [6, 5, 12, 10, 9, 1]이 입력 배열이라고 했을 때, 가장 먼저 [6, 5, 12] 와 [10, 9, 1]로 분리한다.
- [6, 5, 12]는 [6]과 [5, 12]로 분리하고, [10, 9, 1]은 [10]과 [9, 1]로 분리한다. 더 쪼갤 수 있는가?
- [5, 12]는 [5] 와 [12]로 분리하고, [9, 1]은 [9] 와 [1]로 분리한다. 이제 정렬을 시작한다.
- [5]와 [12]를 순서대로 정렬하여 [5, 12]를 반환하고, [9]와 [1]도 정렬하여 [1, 9]를 반환한다.
- [6]과 [5, 12]를 정렬할 때, 맨 앞자리를 비교한다. 왜? 이미 정렬이 된 배열이기 때문에 맨 앞자리가 해당 배열에서 가장 작은 수이기 때문이다. 정렬하면 [5, 6, 12]가 된다. 마찬가지 방법으로 [1, 9, 10]이 정렬되었다.
- 이 부분에서 해당 알고리즘의 효율성을 엿볼 수 있다. 어차피 이미 정렬해서 올라온 배열이기 때문에, 뒤에 있는 수는 상관없이 맨 앞자리 수만 비교하면 된다.
- 두 개의 배열 [5, 6, 12]와 [1, 9, 10]을 병합 정렬한다. 맨 앞자리 수를 비교하여 pop으로 result값에 넣어준다.
2. 병합 정렬의 시간 복잡도
- 병합 정렬의 시간 복잡도는 O(nlogn)로 선택 정렬이나 삽입 정렬의 계산 복잡도 O(n^2)보다 낮다.
- 최악의 경우에도 O(nlogn) 시간 복잡도를 가진다.
3. 일반적인 병합 정렬 알고리즘
def merge_sort(a):
n = len(a)
print("a: {}".format(a))
if n <= 1:
return a
mid = n // 2
g1 = merge_sort(a[:mid])
g2 = merge_sort(a[mid:])
print("g1: {}".format(g1))
print("g2: {}".format(g2))
result = []
while g1 and g2 :
if g1[0] < g2[0]:
result.append(g1.pop(0))
else:
result.append(g2.pop(0))
print('first while: {}'.format(result))
while g1:
result.append(g1.pop(0))
print('second while: {}'.format(result))
while g2:
result.append(g2.pop(0))
print('thrid while: {}'.format(result))
return result
d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5]
print(merge_sort(d))- 오름차순 정렬을 큰 수에서 작은 수 순서대로 나열하는 내림차순 정렬로 바꾸려면 프로그램의 어느 부분을 바꿔야 할까요?
- 첫 번째 while 문의 첫 번째 if문을 수정하였다. (if g1[0] < g2[0]: --> if g1[0] > g2[0]: )
'코린이 > 코딩 기초 & 알고리즘 공부' 카테고리의 다른 글
| [알고리즘] 삽입 정렬 (0) | 2021.08.15 |
|---|---|
| [알고리즘] 선택 정렬 (0) | 2021.08.01 |
| [알고리즘] 순차 탐색 (0) | 2021.08.01 |
| [알고리즘] 재귀함수 - 최대공약수, 피보나치 수열 (0) | 2021.07.17 |
| [알고리즘] 재귀함수 - 팩토리얼 구하기 (0) | 2021.06.20 |
Comments




