Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 좌표거리
- Set
- 도커 레이어
- pyvista
- 동명이인찾기
- 도커
- 귀여운고래
- geojson
- 지하철역좌표
- docker
- GCN
- STL
- 3d데이터
- 이미지빌드
- GNN
- 알고리즘
- GIS
- MESH
- 데이터입수
- 컨테이너
- osmnx
- Python
- 폴더조사
- 파이썬
- geopandas
- 패치분할
- 그리드분할
- python최단거리
- 3d
- graph
Archives
- Today
- Total
이것저것 기록
[python] 데이터 유사성 측정방법 본문
데이터 간 거리를 측정하는 방법에는 여러 가지 방법이 있다.
거리를 측정하는 이유는, 데이터 간 거리가 '유사도'를 나타내기 때문이다.
오늘은 다음 링크에서 소개하는 데이터 유사성 측정방법을 나열해보려고 한다.
towardsdatascience.com/9-distance-measures-in-data-science-918109d069fa
9 Distance Measures in Data Science
The advantages and pitfalls of common distance measures
towardsdatascience.com
머신러닝 (혹은 딥러닝)을 다루게 된다면 데이터들 간 유사도 측정은 거의 필수이기 때문에 이렇게 정리 해놓으면 내가 (혹은 누군가가) 언젠가 유용하게 쓰게 될 거라 믿는다.
1. Euclidean Distance

- 두 점 p, q사이의 유클리디안 거리를 구하면 이 두 점의 최단거리가 된다.
- 다음 코드는 넘파이 라이브러리를 활용하여 두 점 사이의 유클리디안 거리를 이용한 코드이다.
import numpy as np
point1 = np.array((1, 1))
point2 = np.array((2, 2))
dist = np.linalg.norm(point1 - point2)
print(dist) # 1.41421
2. Cosine Similarity

- 코사인 유사도는 내적공간의 두 벡터간 각도와 코사인값을 이용하여 측정된 벡터간 유사한 정도이다. 코사인 유사도는 '방향'에 대한 유사도이다. 즉, '거리'는 고려하지 않는다는 거다.
- 여기서 유클리디안 거리와 코사인 유사도의 차이점이 드러난다. 거리 기반 (ex.유클리디안 거리)은 좌표를 기준으로, 가까운 좌표에 있는 점들이 유사도가 높다고 측정되는 반면, 각도 기반 (ex.코사인 유사도)은 기울기와 방향이 같은 벡터가 유사도가 높다고 측정된다.
- 코사인 유사도는 2차원보다 높은 차원의 데이터, 또 벡터의 크기가 중요하지 않은 데이터에 주로 사용된다.

3. Hamming Distance
- 두 문장 간 편집거리를 측정하기 위한 문자열 메트릭으로, 같은 길이를 가진 2개의 문자열(a, b)을 a에서 b로 바꾸기 위해 몇 개의 글자를 바꿔줘야하는지에 대한 거리이다.
- 해밍거리의 가장 큰 단점은 비교하고자 하는 두 문자의 거리가 같아야한다는 점이다.
- 두 문자의 해밍거리 계산을 위해 XOR 연산을 수행한 후 나온 값에서 1의 개수를 세면 거리가 된다.
- 예를 들어 1101과 1111이라는 문자열이 있다고 가정하자. XOR 연산을 수행하면
- 1101 ⊕ 1111 = 0010 이므로, 해밍거리 d ( 1101, 1111 ) = 1 이다.
4. Manhattan Distance
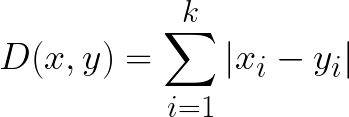
- 맨하탄 거리는 두 점 p, q가 있을 때, 가상 체스보드가 있다고 생각하고 오직 수평, 수직 이동만 하여 p에서 q까지 이동할 때 최단으로 걸리는 거리이다.
5. Chebyshev Distance

- 두 점 p, q간 좌표 차원을 따라 가장 긴 거리를 거리값으로 선택하는 방식이다.
- 식에서도 볼 수 있다시피 max(p, q)라고 써있다. (가장 긴 거리를 사용)
- 유클리디안이나 맨하탄에 비해 사용하는 케이스가 매우 한정적이다.
- 예를 들어, 최소한의 움직임 횟수를 도출하고자 할때 용이할 수 있다. (예를 들어, 4번만 방향을 꺾어서 목표지점에 도달해야하는 경우?)
6. Minkowski Distance
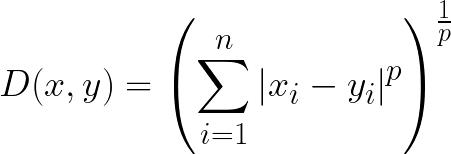
- 민코프스키 거리는 유클리디안 거리와 맨해튼 거리를 일반화한 거리 공식이다.
7. Jaccard Index

- 자카드 인덱스는 두 문장을 각각 단어의 집합으로 만든 뒤, 두 집합의 교집합과 합집합을 활용하여 유사도를 측정하는 방법이다.
- 아래의 그림을 예로 들어보자. 컴퓨터가 예측한 스탑사인은 빨간색 박스이고, 실제 스탑사인은 초록 박스이다. 이때, 자카드 인덱스는 두 박스가 겹치는 부분이 많을수록 그 값이 커지게 된다.

8. Haversine

- 하버사인 거리는 두 점 p, q의 거리를 구할 때 지구의 곡률을 고려하여 거리를 구하게 된다.
- 컴퓨터 자료상 거리가 아닌, 실제 서울-부산의 거리를 구할 때는 단순히 직선거리로 거리를 구해선 안된다. 왜냐하면 지구가 둥근 특성 때문에 곡률이 발생하기 때문이다.
- 그렇기 때문에 만약 지리정보에 관련된 좌표를 다룬다면, 거리를 구할 때 이를 고려해야 한다.
9. Sørensen-Dice Index

- Jaccard Index와 유사한 방식으로 계산이 보다 직관적이고 F1 Score와 유사한 형태로 계산을 한다.
- 영상 분할에 주로 쓰인다. (image segmentation)

'Data Science > ML & DL' 카테고리의 다른 글
| [python, ML] scikit-learn을 사용하여 학습/테스트 데이터 전처리하기 (0) | 2021.04.14 |
|---|---|
| [graph] 그래프 임베딩에 대한 기록 (2) (0) | 2021.01.06 |
| [graph] 그래프 임베딩에 대한 기록 (1) (0) | 2021.01.06 |
| [graph] graphSAGE의 embedding generation algorithm에 대한 기록 (0) | 2021.01.05 |
| [graph] graph pooling에 대한 기록 (0) | 2021.01.01 |
Comments




